Operaciones Binarias son las siguientes

Homenaje a George Boole
Antes de empezar quiero decir unas pequeñas palabras sobre el Creador de las bases mátematicas del binario, George Boole. A veces pequeños gestos, pueden provocar grandes cambios ... hace unos 200 años, Un comerciante de familia relativamente pobre (John Boole) apostó por la educación de su hijo.
Años después, El vastago se habia convertido en el Profesor George Boole, Este Matemático creó algo que en su momento paso casi desapercibido para todo el mundo, salvo para un puñado de matemáticos. George Boole estudió y desarrolló el Algebra de Boole ... una forma de definir el binario que hasta entonces no se habia especificado nunca.
George Boole murió relativamente joven a los 49 años pero su legado es inmortal
100 años después con el advenimiento de la electrónica, La matemática de Boole permitió revolucionar el mundo ... así que desde estas líneas mi más sincero homenaje a este , ya no tan desconocido, matemático que además el año 2015 hizó su 200 aniversario de su nacimiento.
Por cierto, si eres estudiante de binario ya sabes a quien rezarle a san BOOLE ;).
Algebra de Boole
El Álgebra de Boole (o álgebra booleana) es una estructura logico matematica que esquematiza las operaciones lógicas Y, O, NO.
Para ello define tres operaciones regladas para el binario que no existen para el decimal como son los operadores logicos y una serie de reglas que se cumplen en estás operaciones.
Además tambien existen una serie de operaciones adicionales y sus complementarios.
Leyes Binarias
Además para cada operación hay varias leyes que se cumplen y se pueden usar para implementar circuitos o simplificarlos.
- Ley Identidad en Binario
- Ley Conmutativa en Binario
- Ley Asociativa en Binario
- Ley Distributiva en Binario
- Ley de Morgan en Binario
- Ley Doble Negación en Binario
Si A, B y C son variables binarias y consideramos las operaciones
Ley Identidad en Binario
Cada operador al operar con el 1 o el 0 tiene como resultado su anulación.
A AND 0 = 0
A AND 1 = A
A OR 1 = 1
A OR 0 = A
Ley Conmutativa en Binario
El orden de los operandos no cambia el resultado
A AND B = B AND A
A OR B = B OR A
Ley Asociativa en Binario
El orden de asociacion de los operandos no cambia el resultado
(A AND B) AND C= A AND (B AND C) = A AND B AND C
(A OR B) OR C= A OR (B OR C) = A OR B OR C
Ley Distributiva en Binario
Los operadores se pueden distribuir uno respecto del otro
A AND (B OR C ) = ( A AND B) OR ( A AND C)
A OR (B AND C ) = ( A OR B) AND ( A OR C)
Ley de Morgan en Binario
Una negacion sobre varios operandos se puede distribuir en la negacion de los operandos y el operador contrario .
NOT (A OR B ) = (NOT A ) AND (NOT B )
NOT (A AND B ) = (NOT A ) OR (NOT B )
Ley Doble Negación en Binario
La doble negacion se anula.
NOT (NOT A) = A
Puertas logicas en Binario
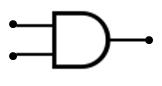
Puerta logica AND
El AND se representa con el signo * en la mayoría de los sitios y coincide con la expresión lógica Y, esto es, el y es verdad si todas las preposiciones lo que une son verdad. (verdad es 1 y falso es 0)
Por ejemplo (el sol es redondo) Y (el sol es amarillo) es verdad ya que ambos son verdad.
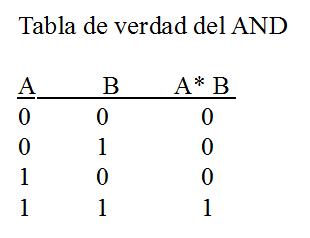
Tabla de verdad del AND
A B A* B
0 0 0
0 1 0
1 0 0
1 1 1
Dibujo de la puerta AND.
La puerta and tiene la parte trasera donde llegan las entradas Recta

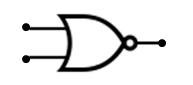
Puerta logica OR
El OR se representa con el signo + en la mayoría de los sitios y coincide con la expresión lógica O, esto es, el OR es verdad si alguna las preposiciones lo que une son verdad. (verdad es 1 y falso es 0)
Se dice que el Or es una condicion debíl ya que con que una de las entradas sea verdad o 1 invalida todas las demas falsas, Por ejemplo la condicion : (el sol es Azul) O (el sol es amarillo) es verdad ya que (el sol es amarillo) es verdad.
Tabla de verdad del OR
A B A+ B
0 0 0
0 1 0
1 0 0
1 1 1
Dibujo de la puerta OR.
La puerta OR tiene la parte trasera donde llegan las entradas Curva.
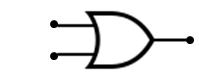
Puerta logica NOT
El NOT es un operador unario , ya que solo tiene una entrada, se representa con el signo - en la mayoría de los sitios y coincide con la expresión lógica NO, esto es, el NO es verdad si la preposiciones de entrada es FALSA. (verdad es 1 y falso es 0)
Por ejemplo NOT (el sol es rojo) es verdad ya que (el sol es rojo) es falso
Tabla de verdad del NOT
A -A
0 1
1 0
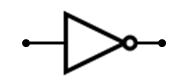
Dibujo de la puerta NOT
La puerta NOT es un triangulo cuya salida es un circulo... en algunos sitios solamente ponen el circulo para representar una entrada negada.
Ademas de las tres principales hay otras tablas de verdad como las siguientes :
Puerta logica NAND
NAND que coincide con una AND Negada. Es muy usada en diseño de circuitos ya que es más facil de hacer que una puerta AND con transistores CMOS .
Ademas por la ley de morgan es facil trasnformar las formulas de un or en una NAND
A OR B = NOT ( NOT A AND NOT B ) = ( NOT A NAND NOT B )
Tabla de verdad del NAND
A B = (A NAND B )
0 0 = 1
0 1 = 1
1 0 = 1
1 1 = 0
La NAND es muy importantes ya que con 4 transistores CMOS podemos hacer una NAND.
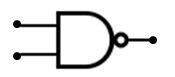
Dibujo de la puerta NAND
El simbolo de La puerta NAND Es igual que la AND tiene la parte trasera donde llegan las entradas pero termina en un circulo para indicar que está negada la salida
Puerta logica NOR
NOR que ademas de ser el grito de guerra de chiquito de la calzada coincide con una OR Negada .
Es muy usada en diseño de circuitos ya que es más facil de hacer que una puerta AND con transistores CMOS .
Además por la ley de Morgan es facil trasnformar las formulas de una Puerta AND en una NOR
A AND B = NOT ( NOT A OR NOT B ) = ( NOT A NOR NOT B )
Tabla de verdad del NOR
A B = (A NOR B )
0 0 = 1
0 1 = 0
1 0 = 0
1 1 = 0
La NOR son muy importantes ya que con 4 transistores CMOS podemos hacer una NOR
Dibujo de la puerta NOR
El simbolo de La puerta NOR Es igual que la OR tiene la parte trasera curva donde llegan las entradas , pero termina en un circulo para indicar que está negada la salida