Guía de Binario
La base matemática en la que reposan todos los principios de la computación moderna se basan en algo tan sencillo como 0 y 1. En este tutorial del binario te vamos a intentar enseñar todos sus secretos.
El binario es un sistema matemático que solo cuenta con dos valores el 0 y el 1, que coinciden con muchos valores que son también dobles y opuestos como encendido y apagado, verdad y falso.
Sobre el binario se definen varias operaciones binarias como el AND , el OR y el NOT con las que podemos hacer operaciones sencillas y en las que se basan todos los ordenadores. Si deseas saber mas sobre las operaciones binarias puedes ver nuestro tutorial sobre el OR y el AND.
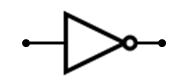
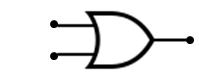
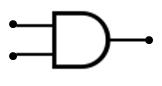
Si deseas saber más sobre las operaciones binarias puedes aprender aqui : > Operaciones binarias
Binario Natural
Binario Complemento a 2
Conversor Binario Complemento a 2 Decimal
Calculadora Decimal Complemento a 2
Binario de punto Fijo
Conversor Binario Fraccionario a Decimal
Calculadora Decimal Binario Fraccionario
Punto Flotante Simple IEEE754
Conversor Flotante Simple IEEE754 a decimal
Calculadora Decimal a Flotante Simple IEEE754
Punto Flotante Double IEEE754
Conversor Flotante Double IEEE754 a Decimal
Calculadora Decimal a Flotante Double IEEE754
Sistema Octal y Hexadecimal
Junto con el binario, se usa muy a menudo otros dos sistemas de numeración que por ser su base múltiplo de dos, es muy fácil transformarlos, son el sistema Octal cuya base es 8 y el sistema hexadecimal cuya base es el 16 y cuya traducción al binario es inmediata. Estos sistemas se usan ampliamente en redes como por ejemplo en las direcciones Mac o IPV6
Los números que están en estos sistemas, se representan con un 8 y un 16 puestos como su indices por ejemplo el numero 173 (8 está en octal y el numero FA3 (16 está en hexadecimal.
Para saber más sobre esto, puedes usar nuestro conversor Decimal a Binario Octal y nuestro conversor Decimal a Binario Hexadecimal en los siguientes enlaces
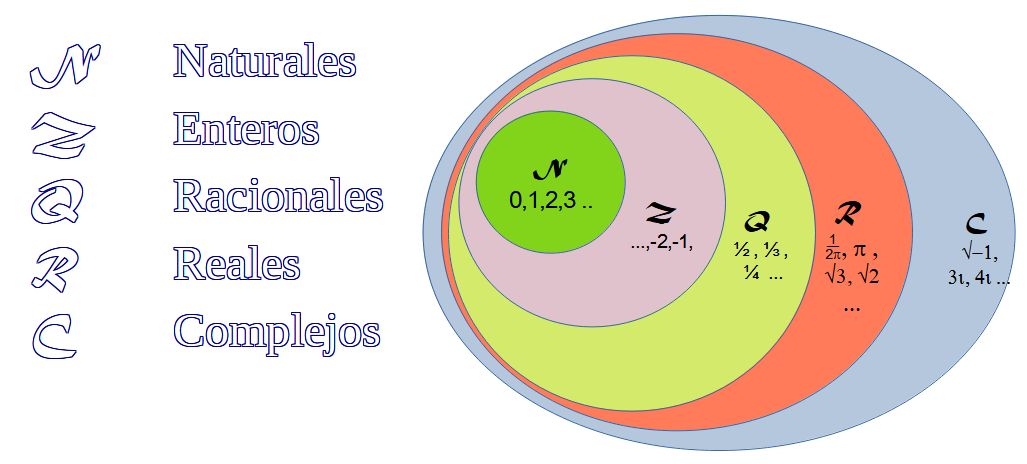
Los Conjuntos de los Números en Binario.
El mundo de los números se pueden imaginar como conjuntos de números, unos incluidos en otros ... el más pequeño es el de los números en Naturales que se representan por N y que son los positivos sin decimales, por ejemplo {0,1,2,3,4 ... } , estos se pueden representar con el binario natural.
Los Enteros son los positivos y negativos sin decimales que se representan con el conjunto Z como por ejemplo {...-3,-2,-1,0,1,2,3,4 ... } , estos se pueden representar con el binario Complemento a 1 y Complemento a 2.
Los numeros Fraccionarios o Racionales son numeros que podemos representar con una fracción y que al final sus decimales acaban siendo finitos o periodicos, esto es se repiten cada cierto numero de iteraciones. Estos números se representan mediante una Q. Estos numeros se pueden representar con el punto fijo o el punto flotante.
Por otro lado tenemos los numeros reales que incluyen todos los démas pero sus numero no tienen que ser periodicos y que pueden tener una cantidad indefinida de decimales como por ejemplo el numero PI o el resultado de la raiz de 2. Estos dos numeros se representan mediante una R para los reales como podemos ver en este gráfico. Estos numeros son un reto para la computación por su tamaño, pero se suelen representar acotados como punto flotante
Binario Natural
El binario Natural es el más básico y aparece al tratar numero naturales, esto es 0,1,2,..
Los números que están en Binario Natural, se representan con un 2 como su subindice, por ejemplo el numero 1010 (2.
El binario se puede convertir al decimal y a la inversa usando unas tecnicas relativamente sencillas que os explicamos en los siguientes enlaces :
Binario para Numeros Negativos
Además del binario natural que sirve para representar números naturales podemos contar con muchos formatos de binario según se necesiten.
Para los números negativos encontramos los formatos de Complemento a Dos y Complemento a Uno. C-2 es la forma más usada en computación de poner un numero binario entero en forma negativa.
Para saber mas sobre esto puedes usar nuestro conversor binario - complemento a dos y nuestro conversor binario - complemento a uno en los siguientes enlaces :
> Conversor Binario Complemento a 1 Decimal
> Conversor Binario Complemento a 2 Decimal
> Calculadora Decimal Complemento a 1
> Calculadora Decimal Complemento a 2
Binario Fraccionario o Punto fijo.
Para representar los números fraccionarios en binario se puede usar el binario fraccionario o de coma fija, El problema es que con el Binario de coma fija es muy dificil representar numeros muy pequeños o muy grandes.
Para saber mas sobre esto puedes usar nuestro conversor Decimal -binario Fraccionario
> Conversor Binario Fraccionario a Decimal
> Calculadora Decimal Binario Fraccionario
Binario Flotante o Binario Punto Flotante.
Para este tipo de Números muy grandes o pequeños, se debe usar un formato llamado la coma flotante o IEEE 754 simple o Doble.Para saber mas sobre esto puedes usar nuestro conversor binario - IEEE 754 y nuestro conversor binario -binario Fraccionario
> Conversor Binario a Flotante Simple IEEE754 a decimal
> Conversor Binario a Flotante Double IEEE754 a decimal
> Calculadora Decimal a Binario Flotante Simple IEEE754
> Calculadora Decimal a Binario Flotante Double IEEE754
¿ Porque usan binario los ordenadores?
a) Resistencia a los errores.
El binario que tiene muchísimas ventajas como su facilidad y su resistencia a los errores.
El sistema binario es un sistema que es muy fácil de usar por solo tener dos valores con los que operar es facilisimo ya que solo hay 4 posibilidades para cada operación ya que solo hay dos símbolos por ello es ideal para los ordenadores.
Otra ventaja del binario es que es muy resistente a los errores pues en electrónica las señales se representan mediante señales electrónicas que pueden variar. En la antigua electrónica analógica (como por ejemplo cuando escuchamos la radio en el coche) la señal depende de su valor en la tensión de manera que si hay un pequeño error toda la señal esta mal. En Digital el valor también depende de la tensión de la señal pero su uso es mucho más sencillo ya que un error no cambiara el valor 0 o 1 a no ser que sea un error enorme.
Ejemplo de señal binaria y su equivalencia
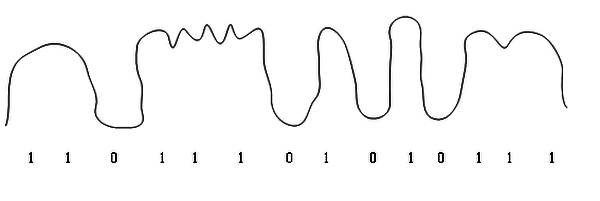
aunque halla muchos errores en la señal el codigo binario no cambia ya que para que cambie tiene que haber un error del 50%.
b) Facil de pasar entre sistemas
Es muy fácil pasar entre binario y decimal para ello solo tenemos que usar una formula iterativa como explicamos en el conversor de binario a decimal.
También es sencillo pasar del sistema decimal al binario para ello solo tenemos que usar una algoritmo muy sencillo que consiste en dividir por 2 y quedarnos con los restos, para ello podemos usar el conversor de decimal a binario.
Con el sistema binario es posible representar todo tipo de números desde números negativos, números con decimales a enormes números flotantes o infinitesimal mente pequeños.
Para números negativos podemos usar formatos como el complemento a uno o el complemento a 2
c) Se puede usar fácil en los ordenadores
Los ordenadores usan unos circuitos que se basan en un componente llamados transistores con los que es muy facil hacer puertas lógicas o operaciones lógicas.
A lo largo del tiempo, los ordenadores se ha ido complicando y por ejemplo el micro de Intel I7 tiene ahora mismo 731 milliones de transistores como podemos ver en la siguiente foto.
d) El binario es muy fácil de Operar.
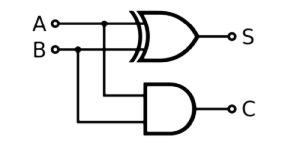
El binario es ideal para los ordenadores, ya que solo tiene dos valores y por ello las operaciones son muy sencillas para sumar. A los circuitos solo hay que implementarle esta tabla que sale como resultado de un circuito llamado semisumador
0+0 = 00
1+0 = 01
0+1 = 01
1+1 = 11
Por estas otras razones el binario es el mejor sistema para usar en el mundo digital.
